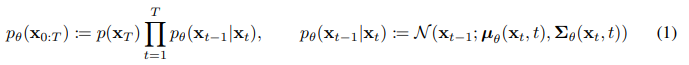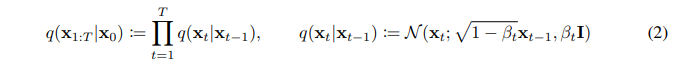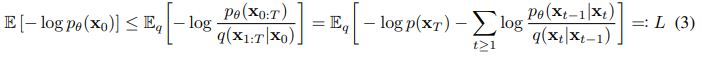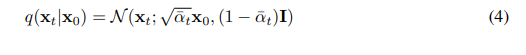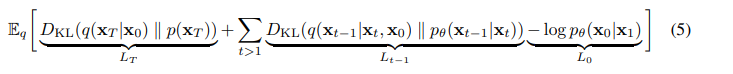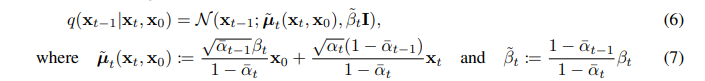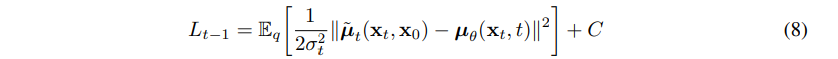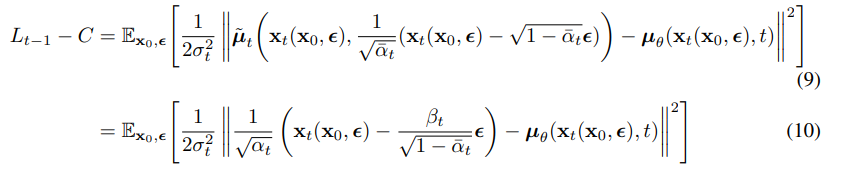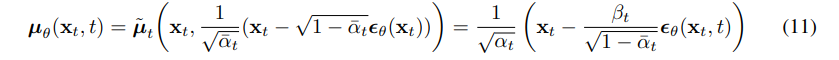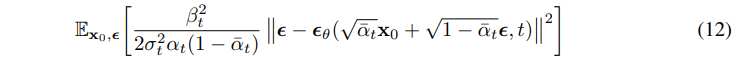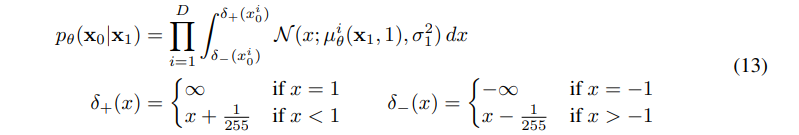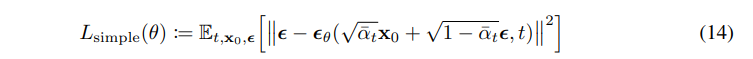Denoising Diffusion Probabilistic Models
论文链接:[2006.11239] Denoising Diffusion Probabilistic Models (arxiv.org)
仓库链接:lucidrains/denoising-diffusion-pytorch: Implementation of Denoising Diffusion Probabilistic Model in Pytorch (github.com)
1 Introduction
DDPM是一个参数化的马尔科夫链,它使用变分推理(variational inference)产生与数据相匹配的样本。
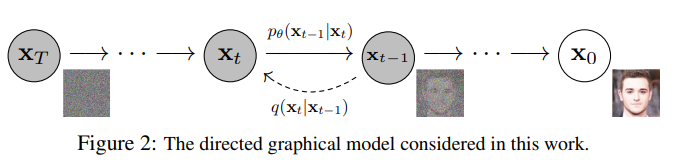
扩散过程(diffusion process)是由左至右的逐渐加噪的过程。我们需要训练逆转该过程所需的马尔科夫链(逆转称为采样过程(sampling process))。如果扩散过程用了高斯噪声,那我们有必要在采样过程加入条件高斯函数,这样有利于参数化。
扩散模型(以下简称为DM)易于定义和训练,但是并没有证据表明其能产生高质量图片。本文的贡献之一在于找到了能产生高质量图片的一种扩散模型参数。
尽管生成的样本质量一般,但我们的模型没有很复杂的对数似然(log likelihood)。我们还发现模型中大部分 lossless codelength 被用于描述难以察觉的图片细节,对此我们用 lossy compression 的语言进行了分析,并揭示了采样过程是一种 progressive decoding,类似于 autoregressive decoding along a bit ordering.
2 Background
获得联合分布 pθ(x0:T) 被称为逆扩散过程(reverse process),其被定义为马尔科夫链,开头是 p(xT)=N(xT;0,I),之后的传递:
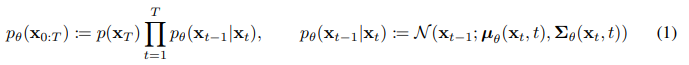
将DM与其他隐变量模型(latent variable model)区分开的,是后验概率 q(x1:T∣x0),这被称作前向过程(forward process)或者扩散过程(diffusion process)。是一个马尔科夫链,逐渐向数据加高斯噪声:
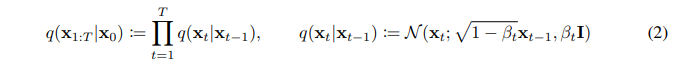
训练方式是优化下面的对数似然:
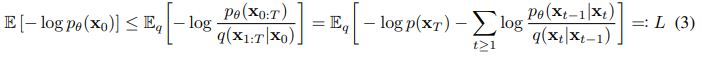
前向过程用到的变量 βt 可以通过重参数化(reparameterization)学习,或者直接作为超参数。此外,前向过程一个显著的性质是它允许在任意时间步 t 上采样 xt,使用记号αt:=1−β, αtˉ:=∏s=1tαs,则有:
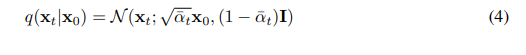
据此将(3)式的损失函数改写为:
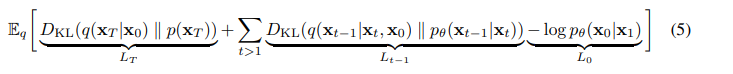
该方程(5)用了KL散度(KL divergence),其中前向过程的后验概率可以用下式计算:
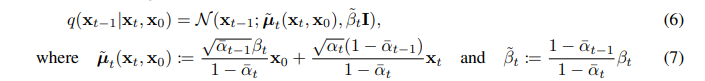
3 Diffusion models and denoising autoencoders
DN看起来就是一类受限的隐变量模型,实际上它在实现上有更高的自由度。我们必须找到前向过程的 βt,以及逆扩散过程的高斯分布参数。为达此目的,我们在3.2节中建立了 DM 和 denoising score matching 之间的联系,从而在3.4节中得到简化的加权的 variational bound 目标。最终,我们的模型在4节中通过简单性和实证结果来证明。
3.1 Forward process and LT
忽略 βt 需要通过重参数化来学习的事实,将他们作为常数。因此,后验概率 q 没有可学习参数,故方程(5) 中 LT 可以作为常量。
3.2 Reverse process and L1:T−1
现在我们讨论 pθ(xt−1∣xt)=N(xt−1;μθ(xt,t),Σθ(xt,t)) ,其中 1<t≤T. 首先我们设置 Σθ(xt,t)=σt2I. 实验中,设置 σt2=βt 以及 σt2=β~t=1−αˉt1−αˉt−1βt 有着相似的结果,前者对于x0∼N(0,I)最优,后者对于被确定地设置为一个点的x0最优。
由于 pθ(xt−1∣xt)=N(xt−1;μθ(xt,t),σt2I),我们可以将(5)式中 Lt−1 改写为:
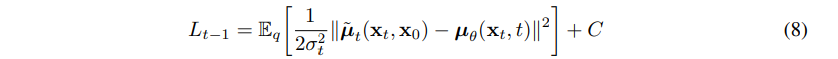
所以我们可以看到最直接的参数化就是用 μθ 去预测 μ~t,也就是前向过程中后验概率的平均值。但也可以从(4)式得到的 xt(x0,ϵ)=αˉtx0+1−αˉtϵ,其中 ϵ∼N(0,I),结合(7)式,将(8)式继续改写为:
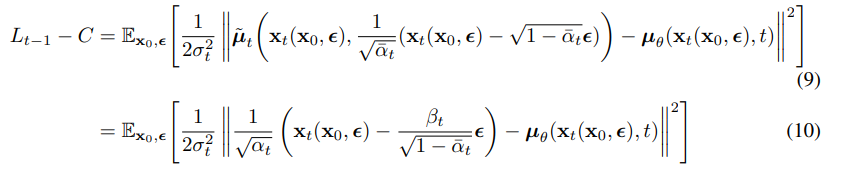
(10)式表明 μθ 需要去预测 αt1(xt−1−αˉtβtϵ). 在逆扩散过程中,xt 是输入,而前向过程中所加的噪声 ϵ 则是未知数。我们选择另一种参数化:
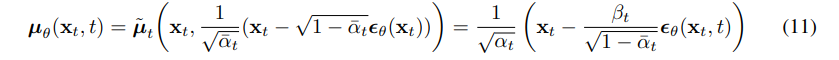
其中 ϵθ 用于预测 xt 时的前向噪声 ϵ. 这样,采样 xt−1∼pθ(xt−1∣xt) 其实就是计算 xt−1=αt1(xt−1−αˉtβtϵθ(xt,t))+σtz,其中 z∼N(0,I). 根据(11)式,我们可以将(10)式简化为:
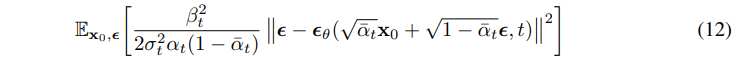
根据(14)式以及 xt 的计算方式,得到如下训练以及采样过程伪代码:

3.3 Data scaling, reverse process decoder, and L0
假设图像数据{0, 1, …, 255}被线性缩放到[-1, 1],这样确保逆扩散过程可以在从标准正态先验概率 p(xT) 开始的一系列一致的输入上进行操作。为获得离散对数似然,对于逆扩散过程最后一步:
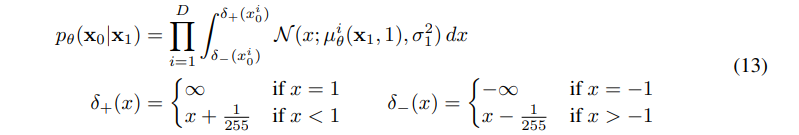
其中D是数据维度,上标i表示提取一个坐标。
3.4 Simplified training objective
综合(12)式和(13)式,我们发现用如下简化的损失函数:
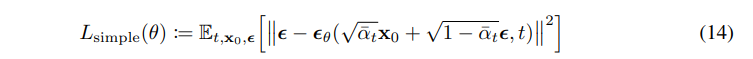
更有利于采样质量,并且实现起来更简单。据此可以得到训练的伪代码。
其他参考资料: